· Meccanica Computazionale

· Metodo degli Elementi Finiti: Teoria Matematica

· INTRODUZIONE AL METODO DEGLI ELEMENTI FINITI

· Andrea Bacchetto

· DESCRIZIONE DEL PROBLEMA

· ASPETTI FONDAMENTALI DEL FEM

DESCRIZIONE DEL PROBLEMA

I fenomeni naturali e le attività umane generano forze, variabili nel tempo, su strutture semplici o complesse. L'analisi del progetto di tali strutture soggette a carichi dinamici costringono a considerare le forze inerziali dipendenti da tempo. La resistenza di una struttura allo spostamento può includere forze che sono funzioni dello spostamento stesso e della velocità. Di conseguenza, le equazioni che governano il moto del sistema sono generalmente equazioni differenziali non lineari alle derivate parziali, ovvero PDEs (Partial Differential Equations) che sono estremamente difficili da risolvere in termini matematici. Di fatto, solo per certe situazioni semplificate si possono ottenere soluzioni analitiche. Fra i metodi analitici più usati per la risoluzione di una PDE vi sono quelli basati sulle Trasformate di Fourier e di Laplace, metodi largamente impiegati nella risoluzione delle equazioni differenziali ordinarie. Il procedimento consiste nel ridurre la PDE in una equazione ordinaria della trasformata di Fourier o di Laplace della funzione incognita. Risolta quest'ultima equazione, l'incognita viene determinata mediante una antitrasformazione.

Per i problemi fisici reali (che implicano complesse proprietà dei materiali, condizioni di carico e condizioni al contorno), invece, quello che si tenta di fare è di introdurre ipotesi ed idealizzazioni necessarie per rendere il problema matematicamente più facile, ma ancora capaci di fornire soluzioni sufficientemente approssimate e risultati abbastanza soddisfacenti dal punto di vista della sicurezza e dell'economia. Il legame tra il reale sistema fisico e la soluzione matematica è fornito dal modello matematico del sistema idealizzato, che include tutte le ipotesi ritenute significative per il sistema reale.

La soluzione delle equazioni del modello matematico viene, attualmente, calcolata attraverso l'impiego di potenti metodi numerici (essenzialmente il Metodo degli Elementi Finiti basato sulla formulazione variazionale) che rendono possibili l'esecuzione dello studio e della progettazione in maniera pratica ed efficace. L'analisi teorica delle tecniche di simulazione numerica e lo sviluppo applicativo dei relativi codici di calcolo all'ingegneria meccanica-strutturale, costituiscono l'oggetto di studio della Meccanica Computazionale delle Strutture.

ASPETTI FONDAMENTALI DEL FEM

Il Metodo degli Elementi Finiti, ovvero FEM (Finite Element Method), è una tecnica dell'Analisi Numerica volta ad ottenere, come anticipato, soluzioni approssimate per una molteplicità di problemi, non solo di Ingegneria Strutturale, ma anche di Fisica, Bioingegneria, Astronomia. Benché originariamente sviluppato per studiare il campo tensionale nelle strutture aeronautiche, è stato poi esteso ed applicato al vasto campo della Meccanica dei continui. Per la sua varietà di impiego e duttilità quale strumento di analisi, è stato sviluppato ed è attualmente utilizzato nelle Università e nell'Industria. In numerosi problemi fisici e ingegneristici risulta sufficiente ottenere soluzioni numeriche approssimate, piuttosto che soluzioni analitiche esatte di difficile utilizzo pratico. Poiché è sempre possibile (sotto certe ipotesi) scrivere le equazioni differenziali e le condizioni al contorno anche di problemi complessi, si può riscontrare tuttavia come non sia sempre possibile trovare una soluzione analitica in forma chiusa, a causa della irregolarità della geometria.

Una possibilità per superare questa difficoltà è quella di fare ipotesi semplificative per ridurre il problema dato ad uno possibile da trattare. Cronologicamente, il primo metodo di Analisi Numerica sviluppato è stato il Metodo delle Differenze Finite ovvero FDM (Finite Differences Method). Tale metodo lascia per così dire inalterato il modello fisico e discretizza le equazioni differenziali del problema. L'algoritmo delle equazioni alle differenze finite aumenta di efficacia al crescere del numero dei punti (dove la funzione è incognita) di intersezione della griglia, che si sovrappone al dominio di definizione della funzione incognita. Con il FDM si possono trattare problemi anche molto complessi (per esempio di Fluidodinamica Numerica). Se tuttavia subentrano geometrie irregolari o particolari condizioni al contorno, tale metodo diventa di difficile applicazione. 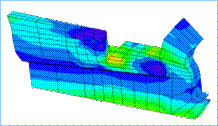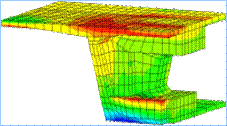Più recentemente il FDM è stato soppiantato dal FEM: contrariamente al primo metodo, che vede il dominio da analizzare come una serie di punti di un reticolo, il FEM vede il dominio come l'unione di tanti sottodomini di forma elementare (vedi Figure 1, 2, 3).

drvlink kneecast dia_res

Figura 1 Figura 2 Figura 3

Sintetizzando, come si è fatto in precedenza, si può dire che, in quest'ultimo caso, le equazioni differenziali vengono lasciate inalterate (relativamente a ciascun elemento finito) mentre il dominio viene discretizzato. In un problema al continuo di qualsivoglia dimensione, cioè in un corpo o in una regione dello spazio in cui abbia luogo un particolare fenomeno, la variabile di campo, come la pressione, lo spostamento, la temperatura, la velocità o la densità, è funzione di ciascun generico punto del dominio di definizione. Di conseguenza il problema presenta un numero infinito di incognite. La procedura di discretizzazione agli elementi finiti lo riduce ad un problema con un numero finito di incognite, suddividendo il dominio in elementi finiti ed esprimendo il campo incognito in termini di funzioni approssimanti, definite all'interno di ogni elemento. Le funzioni approssimanti, chiamate anche funzioni di forma, vengono individuate mediante i valori che la variabile dipendente assume in punti specifici detti nodi. I nodi sono posti di solito sul contorno degli elementi, in punti comuni a due o più elementi. Oltre ai nodi sul contorno un elemento può presentare dei nodi al suo interno. I valori che la variabile di campo assume sui nodi, ne definiscono univocamente l'andamento all'interno dell'elemento. Nella rappresentazione agli elementi finiti di un problema, i valori nodali della variabile di campo rappresentano le nuove incognite.