· Meccanica Computazionale

· Metodo degli Elementi Finiti: Modellazione

· INTRODUZIONE ALLA MODELLAZIONE FEM

· Andrea Bacchetto

· INTRODUZIONE

· Idea di base dell’approssimazione

· DISCRETIZZAZIONE DEL DOMINIO DI INTEGRAZIONE

INTRODUZIONE

Il Metodo degli Elementi Finiti (FEM) nasce in sordina negli anni 60, ma successivamente allo sviluppo degli strumenti informatici, ha una evoluzione ed uno sviluppo esponenziali, suscitando notevole interesse per il vasto numero di campi cui è possibile applicare i suoi principi. L’uso del FEM si afferma come uno dei migliori strumenti per l’indagine quei sistemi complessi, per i quali indagini e sperimentazioni in laboratorio comporterebbero spese eccessive, difficoltà logistiche e difficoltà legate alla misurazione fisica delle varie grandezze.

Se i primi approcci automatici per la soluzione delle equazioni differenziali che governano i fenomeni fisici, si affermano con le differenze finite, il FEM evolve le possibilità di soluzione dando una possibilità di applicazione che non ha eguali, grazie alla sua inoppugnabile flessibilità.

La generalità del metodo, inizialmente sviluppato dagli ingegneri e successivamente dimostrata anche dai matematici, ha permesso moltissimi studi ed applicazioni, aprendo la strada a nuovi filoni di ricerca che attualmente affrontano problematiche di notevole interesse di natura teorica e pratica.

Idea di base dell’approssimazione

L’idea base dell’approssimazione usata nel metodo agli elementi finiti è quella di approssimare il vero andamento della funzione incognita con quello di alcune funzioni particolari ad andamento noto: generalmente polinomiali, ma anche trigonometriche ed esponenziali. Vengono presi in considerazione un numero limitato di punti (chiamati anche nodi) interni al dominio di integrazione, per i quali i valori della funzione approssimata risulteranno identici a quelli della funzione approssimante.

A supporto di tale affermazione citiamo il teorema di Weierstrass per il quale se una funzione f è continua nell’intervallo [a,b] fissato un arbitrario e > 0, esiste un polinomio P(x) tale che:

(1)

Cioè ogni funzione continua può essere sufficientemente approssimata da un polinomio di grado sufficientemente elevato

È evidente come l’approssimazione lineare, che risulta essere quella più semplice, è anche quella peggiore nella qualità dell’approssimazione stessa. In accordo con il teorema di Weierstrass, infatti, l’ordine del polinomio utilizzato nell’approssimare la soluzione reale, infatti, influisce sulla precisione con cui si potranno valutare la soluzione delle equazioni differenziali: più è elevato il grado, migliore sarà l’approssimazione.

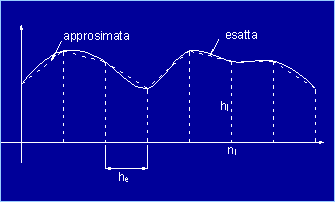
Figura 1

In Figura 1 è mostrato chiaramente il principio di base utilizzato nel metodo FEM: una volta suddiviso il dominio di integrazione in intervalli (che possono essere anche non regolari), si procede ad approssimare la funzione incognita con delle funzioni ad andamento noto, scegliendo, come incognite del problema trattato, i soli valori ai nodi (h_j). Dalla soluzione delle equazioni algebriche si otterranno i valori nodali del campo approssimato; quelli interni agli intervalli vengono valutati in base alle funzioni di approssimazione utilizzate.

Precisione dell’approssimazione

È necessario sottolineare come la precisione dell’approssimazione dipenda, oltre che dal grado del polinomio utilizzato, anche dalla dimensione dell’intervallo di suddivisione: mantenendo, ad esempio, un polinomio lineare, l’errore si riduce nella misura in cui vengono ravvicinati i nodi e quindi di quanto vengono ridotti gli intervalli.

Risulta evidente a questo punto come nel caso di presenza di forti gradienti (pendenze) della funzione da approssimare, risulti necessario infittire i nodi solo in tale zona piuttosto che in tutto il dominio della stessa. Tale potente flessibilità è uno dei maggiori vantaggi del FEM rispetto al FDM.

Perché “Elementi Finiti” ?

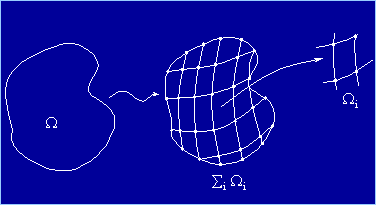
Il termine elementi finiti fu utilizzato in un articolo di Clough del 1960 dove il metodo fu presentato per la soluzione di uno stato piano di tensione. Il termine deriva dal fatto che il dominio di integrazione viene suddiviso in un determinato numero di sotto-domini (vedi Figura 2), all’interno dei quali le equazioni differenziali che governano il problema vengono risolte in maniera approssimata nel senso espresso sopra.

Figura 2

DISCRETIZZAZIONE DEL DOMINIO DI INTEGRAZIONE

Uno dei passi più importanti dell’analisi strutturale è l’idealizzazione della struttura che permette di passare dal modello fisico a quello numerico. Tale passaggio comporta la riduzione del numero di gradi di libertà che nel mezzo continuo sono infiniti, mentre, considerando solo alcuni punti (nodi) della struttura, sono in numero, per l’appunto, finito.

Si parla allora di discretizzazione della struttura come quell’operazione che permette di passare dalla struttura reale e quella idealizzata / approssimata / discretizzata per la quale è possibile applicare il metodo degli elementi finiti al fine di ottenere una soluzione ingegneristica del problema.

Sapendo inoltre che la soluzione mediante l’utilizzo di metodi numerici avviene per mezzo di calcolatori elettronici, l’idea della discretizzazione è legata al limite fisico che tali macchine possiedono a livello di immagazzinamento di dati (memoria). Nonostante l’evoluzione della tecnologia degli elaboratori abbia permesso di risolvere oggi dei problemi che qualche decennio fa erano ingestibili per la grossa mole di spazio fisico necessario per memorizzare dati di input e dati di output, la realizzazione del modello numerico risulta essere tuttora un problema non ancora risolto in via definitiva.

La modellazione della struttura costituisce quindi uno dei passi più importanti dell’analisi strutturale, in quanto in questa fase vengono infatti formulate diverse ipotesi che permetteranno la semplificazione del modello reale: i risultati saranno influenzati da queste assunzioni, che comunque, una volta note, permetteranno una corretta interpretazione dei valori numerici.

Una breve introduzione alle molle

Prima di passare alla vera e propria discretizzazione delle strutture, una nota sulle molle a comportamento elastico lineare è d’obbligo: esse infatti rappresentano uno dei più importanti punti di riferimento per la comprensione del comportamento di una struttura anche complessa. Dall’impostazione classica dello studio delle strutture è usuale, infatti, schematizzare i corpi con un insieme di molle. 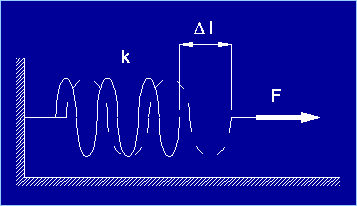Tali molle possono essere di tipo traslazionale o rotazionale a seconda che debbano rappresentare gradi di libertà legati a spostamenti o rotazioni.

La sollecitazione di sforzo assiale, ad esempio, può essere rappresentata mediante una molla traslazionale (vedi Figura 3).

Figura 3

La sollecitazione a momento flettente trova invece la sua più semplice rappresentazione in una molla rotazionale (vedi Figura 4), il cui valore di momento sviluppato è pari al prodotto della rigidezza e della variazione di apertura angolare (M=k_jj).

Alcuni principi e regole di base sono importanti al fine di un corretta comprensione di una struttura e la sua possibile evoluzione a seguito dell’applicazioni dei carichi.

Figura 4

Consideriamo ora una semplice molla traslazionale a comportamento lineare:

(2)

dove k è la rigidezza della molla, Dl è l’allungamento della molla rispetto alla posizione di partenza (cioè in condizione scarica) e F è la forza che è necessario applicare alla molla per deformarla di Dl o, viceversa, la reazione che il vincolo della molla deve esplicare a seguito di un allungamento pari a Dl.

L’importanza dell’argomento molle è presto dimostrata: si parla infatti di rigidezza di una struttura e di matrice di rigidezza, intendendo quella funzione di trasferimento del sistema dall’insieme delle forze applicate a quello degli spostamenti indotti. Per un sistema non più governato da un’unica molla, e quindi non più da un solo grado di libertà, ma da un insieme di molle, che rappresentano i vari gradi di libertà che possiede un corpo, la relazione diventa la seguente:

(3)

dove K è l’operatore lineare detto anche matrice di rigidezza, U è, nello spazio vettoriale di arrivo, il vettore delle incognite e f è, nello spazio vettoriale di partenza, il vettore dei termini noti. È degno di nota vedere inoltre come la scrittura formale dei problemi descritti in (2) e (3) si presenti molto simile, potendo quindi attribuire a k e a K un significato analogo, facilitando in tale maniera il comportamento globale di una struttura.