· Meccanica Computazionale

· Analisi FEM-BEM nella Meccanica delle Strutture

· ANALISI NON LINEARE DI STRUTTURE IN CA E CAP *

· Marco Bozza

· INTRODUZIONE

· TIPI DI NON LINEARITÁ

· PROCEDURA PER L'ANALISI NON LINEARE

* L’articolo riporta alcuni brani del Prof. Aldo CAUVIN e del Prof. Giuseppe STAGNITTO, entrambi della Facoltà di Ingegneria dell’Università di Pavia, tratti dal testo "Analisi limite e non lineare di strutture in calcestruzzo armato", Collana di Ingegneria Strutturale - N. 10, Edizioni CISM

INTRODUZIONE

Il comportamento non lineare delle strutture, che si esprime analiticamente nella non linearità delle equazioni di equilibrio e quindi nella non proporzionalità fra azioni e stato di sollecitazione, è dovuto, oltre agli effetti del secondo ordine che si manifestano in modo evidente nelle strutture snelle, a una serie di fenomeni dovuti ai materiali, che possono essere così riassunti:

Fenomeni in campo elastico

- fessurazione (dovute alla notevole differenza fra resistenza a compressione e resistenza a trazione del calcestruzzo);

- effetti della non linearità della legge costitutiva in campo elastico.

Fenomeni in campo elasto-plastico

- comportamento elasto-plastico dei materiali (acciaio);

Fenomeni in campo viscoso

- deformazioni del materiale nel tempo sotto l'azione di carichi di lunga durata (calcestruzzo).

Come conseguenza di tali fenomeni, avviene nella struttura considerata una ridistribuzione di sollecitazioni che spesso è tale da alterare completamente i risultati dell'analisi lineare elastica, che viene convenzionalmente assunta come base per i calcoli di progetto e di verifica. Di qui la necessità di disporre di strumenti di calcolo che consentano di simulare il comportamento non lineare e, nello stesso tempo, se possibile, siano sufficientemente pratici ed economici da poter essere utilizzati quali strumenti operativi.

TIPI DI NON LINEARITÁ

Non linearità per materiale

Il comportamento non lineare del materiale può essere rappresentato essenzialmente in due modi:

- a livello di legge costitutiva, cioè mediante il legame sforzi-deformazioni ricavato sperimentalmente dal materiale base;

- a livello di diagrammi momenti-curvature.

In questo caso il legami sforzi-deformazioni è espresso a livello "macroscopico" dal legame sollecitazione (momento) - spostamento (curvatura), con riferimento ad una determinata sezione della struttura considerata. Inoltre devono essere implicitamente adottate determinate ipotesi sul comportamento dell'elemento strutturale cui il diagramma si riferisce. Nella definizione della rigidezza degli elementi finiti può essere fatto riferimento sia all'uno che all'altro criterio.

Non linearità per geometria

Le strutture snelle e soggette ad azioni di compressione possono essere sensibili ad effetti non lineari di tipo geometrico, e quindi a pericolo di collasso per instabilità.

Casi in cui è opportuno far ricorso all'analisi non lineare

Si elencano di seguito alcuni casi in cui gli effetti non lineari sono particolarmente rilevanti e quindi in cui è consigliabile, e talvolta necessario, far ricorso all'analisi non lineare:

- valutazione della capacità portante di strutture esistenti danneggiate;

- analisi di strutture snelle;

- autotensioni dovute a variazioni termiche e a distorsioni impresse;

- analisi sismica;

- casi in cui si hanno forti ridistribuzioni di momento in fase fessurata (travi continue in CA, travi in curva, muri accoppiati di controventamento);

- strutture molto deformabili in esercizio.

PROCEDURA PER L'ANALISI NON LINEARE

La simulazione numerica del comportamento non lineare delle strutture può essere affrontato a diversi livelli di complessità:

- tipo di elemento finito

- leggi costitutive dei materiali

- tipo di analisi

- procedimenti numerici di calcolo

- storia del carico

- livello di analisi

Tipo di elemento finito

Il tipo di elemento finito adottato definisce la complessità del modello matematico. L'analisi di strutture monodimensionali in regime non lineare può essere effettuata a diversi livelli di esattezza, così classificabili:

livello macroscopico

la rigidezza dell'elemento viene determinata sulla base di una legge momenti-curvature costruita con opportuni criteri.

livello microscopico semplificato

Immaginando, ad esempio, di suddividere una trave in strati longitudinali, ad ogni strato corrisponde un modulo elastico dedotto dalla legge costitutiva del materiale in corrispondenza della deformazione longitudinale subita dallo strato stesso.

livello microscopico

si utilizzano elementi bi o tridimensionali che simulano a livello locale il comportamento strutturale.

Leggi costitutive dei materiali

La distinzione riguarda essenzialmente l'uso di leggi olonome (identiche in fase di carico e di scarico) e anolonome (aventi andamenti diversi nei vari cicli di carico e scarico).

Tipo di analisi

Il calcolo non lineare può essere effettuato sia in fase statica che dinamica. In quest'ultimo caso è necessario ricorrere all'integrazione numerica per via diretta dell'equazione dell'equilibrio dinamico.

Procedimenti numerici di calcolo

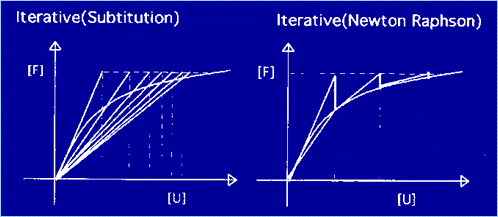
Il fatto che la rigidezza strutturale sia funzione dello stato deformativo fa sì che il sistema di equazioni di equilibrio che regge il problema sia non lineare. Nasce quindi il problema della risoluzione numerica di detto sistema. I vari metodi possono essere classificati in tre categorie:

· Metodi iterativi o "secanti"

In questi metodi si opera a carico costante. Il modo più facile di procedere iterativamente è per successive sostituzioni (Figura 1), utilizzando l'equazione ricorrente:

(1)

essendo F il vettore dei carichi, [K] la matrice di rigidezza globale della struttura, U il vettore degli spostamenti.

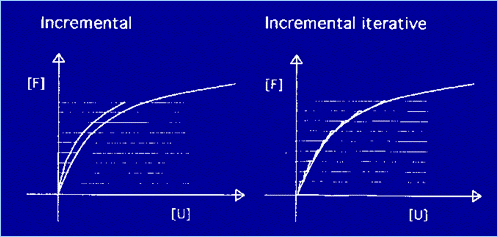
Figura 1

La (1) rappresenta l'equilibrio strutturale globale approssimato all'n-esimo ciclo di iterazione. In tale equilibrio si utilizza la rigidezza calcolata nel ciclo precedente n-1. Per accelerare la convergenza può essere usato il classico metodo di Newton-Raphson. In tale metodo si calcola ad ogni ciclo il carico di equilibrio presente in tale ciclo. La parte di carico eccedente viene applicata alla struttura nel ciclo successivo, calcolando l'incremento di spostamento associato a tale carico ipotizzando per la struttura la rigidezza (tangente) funzione dello stato deformativo precedentemente calcolato. La procedura viene ripetuta finché il carico non equilibrato si riduce ad un valore trascurabile.

· Metodi incrementali o "tangenti"

Nel metodo incrementale si procede applicando per passi il carico secondo una legge prefissata, aggiornando ad ogni passo, in funzione dello stato deformativo raggiunto nel passo precedente, la matrice di rigidezza tangente. Ad ogni incremento di carico viene risolta la seguente equazione di equilibrio:

(2)

Lo stato deformativo finale si ottiene sommando gli incrementi relativi ai vari passi (Figura 2).

Figura 2

· Metodi incrementali-iterativi

L'errore di linearizzazione, implicito nella linearizzazione effettuata ad ogni passo, può essere ridotto aumentando il numero degli incrementi ed anche utilizzando un procedimento iterativo all'interno di ciascun passo. E' questo il procedimento più usato nei codici di calcolo non lineare, in quanto associa ad una ragionevole esattezza la flessibilità d'uso in termini di storia di carico propria del metodo incrementale.

Storia del carico

La soluzione di un sistema non lineare di equilibrio può, a differenza del caso di analisi lineare, non essere unica in quanto può dipendere dalla "storia" di carico applicata alla struttura. Per individuare la soluzione più aderente alla realtà fisica è necessario adottare procedure risolutive di tipo incrementale che siano in grado di seguire, nel limite del possibile, detta storia di carico.

Livello di analisi

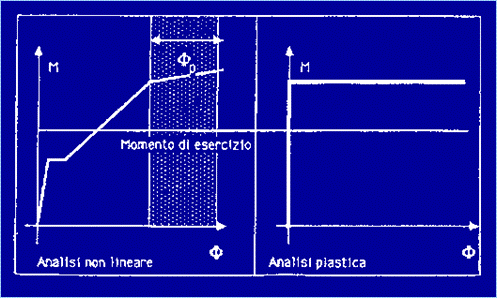
Il livello di analisi fa riferimento ai tipi di non linearità dovuti al materiale effettivamente considerati nell'analisi, e viene meglio descritta con riferimento al diagramma momento-curvatura (o rotazione) di una generica sezione inflessa o presso-inflessa (Figura 3).

Figura 3

La semplificazione più drastica che può essere fatta è quella di ipotizzare per il materiale un comportamento rigido-plastico. In tal caso il diagramma momento-curvatura si riduce ad una bilatera con un tratto verticale (tratto rigido). Su tale ipotesi è basato il calcolo plastico.

Una semplificazione di portata più limitata può essere introdotta adottando come stato limite ultimo convenzionale quello corrispondente alla formazione della prima cerniera plastica in una sezione critica. In tal caso si effettua un'analisi non lineare "elastica", in quanto il solo fenomeno non lineare che viene simulato è (oltre eventualmente agli effetti del secondo ordine) l'eventuale fessurazione del materiale. Il diagramma momenti-curvature si riduce a una bilatera (tratto elastico non fessurato, tratto elastico fessurato).

Un'analisi più completa, infine, porta a considerare anche il terzo lato del diagramma momento-curvatura, corrispondente al comportamento in fase plastica del materiale: è così possibile valutare le capacità di resistenza della struttura in fase elasto-plastica fino al collasso effettivo della stessa.

E' importante far notare, per concludere, che solo mediante un'analisi non lineare è possibile effettuare verifiche attendibili di una vasta gamma di strutture. A poco giova far ricorso a mesh con elementi particolarmente sofisticati se poi il comportamento reale del materiale viene schematizzato in modo grossolano dalla legge di Hooke