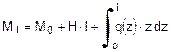PROGETTO DI PONTI E VIADOTTI - INSTABILITA' DELLE PILE ALTE

· Progetto e Sperimentazione di Strutture

· Progetto di Ponti e Viadotti

· INSTABILITÁ DELLE PILE ALTE

· Marco Bozza

· INTRODUZIONE

· SCHEMI STATICI DELL’IMPALCATO

· EFFETTI DEL SECONDO ORDINE

· EVOLUZIONE DEGLI SCHEMI STATICI

· METODI DI VERIFICA

INTRODUZIONE

Nell'iter progettuale di ponti e viadotti, la necessità di contenimento del peso proprio, di riduzione di costi relativi al trasporto dei materiali ed all'acquisizione delle attrezzature costruttive, nonché esigenze di impatto ambientale, orientano i progettisti verso soluzioni strutturali avanzate, con sfruttamento limite dei materiali e delle forme. Inoltre, l'esigenza di svincolare la costruzione degli impalcati dall'impiego di onerosi sostegni a terra ha portato al diffondersi della prefabbricazione e, per le grandi luci, alla messa a punto di varie tecniche, tutte finalizzate ad evitare le centine. La stessa esigenza ha stimolato importanti innovazioni anche nella costruzione delle pile: le casseformi scorrevoli e quelle a ripresa autoportanti.

Le moderne tecniche di costruzione di ponti e viadotti consentono attualmente la realizzazione di opere molto snelle per l'attraversamento di valli e fiumi, con luci di campate elevate e pile molto alte. Queste ultime possono facilmente raggiungere altezze di 60¸120 m, per arrivare fino anche a 190 m. Normalmente le pile hanno profili con caratteristiche di rigidezza variabili lungo l'altezza. Le sezioni trasversali possono essere a cassone, mono o pluricellulari, con spessore delle pareti bruscamente variabile o con profilo variabile con continuità. Poiché molto spesso le pile dei ponti a travata sono alte rispetto alle dimensioni della loro sezione trasversale, devono essere presi in considerazione i fenomeni di instabilità flessionale e locale.

SCHEMI STATICI DELL’IMPALCATO

Per queste strutture si presenta allora il problema impegnativo di valutare lo stato tensionale e deformativo delle pile alte, sia per il corretto esercizio delle stesse, sia per una valutazione affidabile delle loro capacità resistenti ultime. Nello stato limite ultimo, in particolare, è necessario considerare tutti gli schemi resistenti che possono essere mobilitati quando gli spostamenti della pila superano ampiamente quelli massimi di esercizio. A tale scopo è di fondamentale importanza lo schema statico dell'impalcato sulle pile. L'impalcato dei viadotti può assumere due tipologie classiche di schemi statici:

- impalcato con travi in semplice appoggio

- impalcato a travata continua

Impalcato con travi in semplice appoggio

Questo schema è rappresentato da una successione di travi appoggiate, vincolate longitudinalmente con cerniere alternate a carrelli. Trasversalmente è sempre presente un appoggio fisso, che però non vincola i moti relativi di una pila rispetto all'altra. Le problematiche connesse a questo tipo di schema statico mostrano che:

- per ogni pila la condizione di vincolo in direzione longitudinale è simile alla condizione di vincolo trasversale;

- i carichi permanenti agiscono ad eccentricità non nulla;

- il carico del traffico su una sola campata aumenta l'eccentricità:

- in generale la pila risulta soggetta a stati di sollecitazioni biassiali.

Impalcato a travata continua

Questo schema è rappresentato da una travata unica con appoggi fissi su una spalla e vincoli mobili longitudinalmente sulla testa delle pile. In questo schema, nella direzione ortogonale a quella di marcia gli spostamenti della pila sono limitati dal ritegno elastico afferto dall'impalcato. Tale ritegno agisce sia come vincolo elastico estensionale a causa della rigidezza flessionale afferta dall'impalcato in tale direzione, sia come vincolo elastico rotazionale a causa della rigidezza torsionale dell'impalcato, sempre che non si abbiano appoggi singoli che rimandano gli effetti torcenti alle testate. Sebbene questi effetti irrigidenti offerti ad una pila dipendano non solo dalle caratteristiche geometriche e meccaniche dell'impalcato, ma anche da quelle delle altre pile, nondimeno normalmente gli effetti del secondo ordine sono in questo caso meno marcati che nel caso di travi su due appoggi. Per gli impalcati continui si osserva che:

- per ogni pila la condizione di vincolo in direzione longitudinale è diversa dalla condizione di vincolo trasversale sulla pila. In particolare, l'impalcato continuo esercita sempre un'azione di ritegno trasversale sulla pila;

- sia i carichi permanenti, sia il carico del traffico, qualsiasi esso sia, non alterano l'eccentricità nella direzione longitudinale dell'impalcato, che è funzione della posizione istantanea dell'appoggio mobile;

- negli schemi mono-appoggio sulle pile centrali, e torsione rimandata alle testate, è presente la sola eccentricità nella direzione di marcia.

EFFETTI DEL SECONDO ORDINE

Normalmente, l'analisi delle strutture a sviluppo verticale viene condotta facendo riferimento alla loro configurazione indeformata, con il carico agente lungo l'asse verticale indeformato della struttura. Tuttavia, nel caso delle pile, lo sbandamento prodotto dalle azioni applicate dà luogo ad un'eccentricità del carico assiale, che induce un incremento del momento flettente presente sull'elemento strutturale. Questo momento flettente addizionale è detto momento del II ordine e, nel caso di colonne sufficientemente snelle, ha un'influenza non trascurabile sia sulla deformabilità in esercizio, sia sulla capacità resistente ultima della struttura. Per tenere conto di questo fenomeno (effetti del II ordine) si deve allora calcolare lo stato di sollecitazione, nota che sia la configurazione deformata, che a sua volta dipende dallo stato di sollecitazione della struttura. Questo tipo di approccio implica una risposta non lineare della struttura, indipendentemente dalle caratteristiche dei materiali costituenti la pila. Ciò è causato dal fatto che la relazione tra i parametri di sollecitazione interni e il carico applicato non è lineare. Va osservato che gli effetti del secondo ordine (non linearità geometrica) sono significativi se producono frecce dell'ordine di qualche unità percentuale rispetto all'altezza della pila. Per questo motivo l'Eurocodice 2 propone di non considerare la non linearità geometrica solo se produce una riduzione della capacità resistente della pila inferiore al 10%, ma questo si verifica solo se le frecce sono significative. Finché la pila presenta una bassa deformabilità rispetto alla sua capacità resistente, è possibile allora trascurare gli effetti del secondo ordine. Quando tuttavia ciò non accade le pile da ponte devono essere considerate snelle e verificate all'instabilità. Tali verifiche sono rese complesse dal comportamento non lineare dei materiali costituenti le pile (calcestruzzo e acciaio), per cui nel complesso esse dovranno tenere in considerazione effetti del secondo ordine (non linearità per geometria) e leggi costitutive non lineari (non linearità per materiali).

Insieme agli effetti del secondo ordine, il comportamento reale di una pila da ponte in calcestruzzo armato deve considerare anche i seguenti fattori:

- forma della sezione trasversale;

- leggi costitutive dei materiali;

- imperfezioni geometriche;

- distribuzione delle azioni interne;

- imperfezioni di natura meccanica;

- effetti della viscosità del cls nel tempo.

Insieme a questi fattori, l'analisi strutturale globale delle pile deve poi prendere in considerazione le seguenti azioni:

- carichi assiali derivanti dallo schema statico complessivo del ponte;

- azione assiale variabile per effetto del peso proprio;

- cedimenti e rotazioni delle fondazioni;

- azioni termiche;

- azioni del vento;

- azioni sismiche;

- effetti differiti nel tempo;

- eccentricità biassiale.

EVOLUZIONE DEGLI SCHEMI STATICI

Per com'è concepito e realizzato il sistema strutturale impalcato-pile dei viadotti, lo schema statico delle pile può subire un processo di evoluzione. Per questo motivo la schematizzazione di una pila alta, inserita nel sistema strutturale di un viadotto, deve poter interpretare in modo aderente sia le caratteristiche dei vincoli che la collegano all'impalcato, sia i cinematismi di progetto che questi possono consentire. Va infatti considerata l'eventualità che in direzione longitudinale possa verificarsi un'evoluzione dello schema statico: in una prima fase può sussistere lo schema a mensola (fase di costruzione dell'impalcato) sino a quando il cinematismo consentito dai vincoli e dai giunti non si esaurisce. Successivamente, l'impalcato può bloccare lo sbandamento della sommità delle pile variando ancora lo schema statico (questo nell'ipotesi che il dispositivo di fine corsa degli appoggi sia in grado di garantire l'azione di vincolo del sistema variato). Va osservato che nelle pile molto alte lo stato limite di deformazione è normalmente più oneroso che lo stato limite ultimo di resistenza e stabilità, in quanto le frecce significative (per effetti del secondo ordine) non sono generalmente compatibili con le condizioni normali di esercizio del ponte. Nondimeno, anche la verifica dello stato limite di deformazione, per essere affidabile, deve essere svolta adottando, sotto le combinazioni di esercizio dei carichi, le stesse procedure non lineari proposte per le verifiche agli stati limite ultimi. Per questa però il comportamento dei dispositivi di vincolo è quello tipico della situazione di esercizio, mentre, nella verifica allo stato limite ultimo di resistenza e stabilità, l'adozione di ipotesi semplificative permette ugualmente di garantire i livelli di sicurezza strutturali richiesti. In ogni caso i risultati vanno inquadrati e interpretati nel contesto reale, confrontando gli spostamenti ottenuti con le possibilità cinematiche offerte dal sistema pila-vincoli-impalcato.

In generale il processo di evoluzione dello schema statico implica l'adozione di vincoli posticipati e considera la non linearità dei materiali, che rende la distribuzione delle rigidezze funzione del livello di sollecitazione. Per questo motivo la determinazione delle reazioni iperstatiche dei vincoli, antecedenti e posticipati, ha carattere iterativo. Si deve in aggiunta tenere conto anche della dipendenza delle rigidezze, e quindi dello stato di sollecitazione, dalla configurazione deformata della struttura (effetti del secondo ordine). Quello che nel complesso quindi si dovrebbe eseguire è un'analisi non lineare dei telai snelli che tenga conto delle numerose condizioni di carico da affrontare, e per la cui definizione manca il supporto delle linee di influenza, con l'incertezza del comportamento dei vincoli.

METODI DI VERIFICA

I metodi di verifica delle pile alte possono essere raggruppati in due categorie:

- metodi di tipo generale;

- metodo della colonna modello,

- metodo del carico critico euleriano.

Metodi di tipo generale

I metodi di tipo generale sono basati su modellazioni numeriche globali delle strutture, mediante codici agli elementi finiti. Questi programmi consentono di eseguire vari tipi di verifica: statiche, dinamiche, di buckling (instabilità). I vantaggi che derivano dall'utilizzo di queste tecniche sono costituiti principalmente dalla possibilità di eseguire analisi strutturali in regime non lineare, considerando contemporaneamente le non linearità per geometria e per materiali, con condizioni al contorno del tutto generali.

Metodo della colonna modello

Tra i metodi approssimati, quello che permette un'agile e rapida soluzione del problema dell'instabilità è il cosiddetto metodo della colonna modello. Questo metodo, oltre ad essere ammesso dalla normativa italiana, si basa sull'utilizzo di tabelle che riducono al minimo l'onere di calcolo.

Questo metodo presuppone che la configurazione deformata della pila sia assimilabile ad un arco sinusoidale del tipo:

(1)

essendo "a" la freccia in sommità della pila nella configurazione deformata, e "l" l'altezza della pila. Ovviamente si considerano distribuzioni di carico tali da dare origine ad una configurazione deformata che sia approssimativamente sinusoidale. In altre parole sono escluse le configurazioni di carico per le quali il momento flettente del primo ordine cambia segno. Derivando due volte la (1) rispetto a z si ottiene, nell'ipotesi di piccoli spostamenti, l'espressione della curvatura c alla generica quota z:

(2)

Nella sezione di base (z = 0):

(3)

da cui:

(4)

con R₀ = R(0). La (4) esprime il legame lineare tra la curvatura nella sezione di base e la freccia in sommità. Questa permette di esprimere il momento del secondo ordine M_II alla base della pila come funzione lineare della curvatura nella stessa sezione. Il momento totale vale allora:

(5)

essendo:

(6)	Momento del primo ordine
(7)	Momento del secondo ordine

Nella (6) M₀ e H sono, rispettivamente, il momento e una forza concentrata orizzontale applicati in sommità, mentre q(z) è un carico distribuito lungo l'altezza della pila (carico del vento). Nell'ipotesi che la sezione, la sua armatura e l'azione assiale P siano costanti lungo l'altezza della pila, la sezione di base è quella più sollecitata. In questo caso la verifica di resistenza e stabilità della colonna può essere effettuata confrontando il momento totale M (relazione (5)) con la capacità resistente della sezione, calcolata per N = P. Questa operazione può essere svolta graficamente tracciando il diagramma momento-curvatura della sezione di base per N = P, rappresentante la risposta della sezione ad un arbitrario momento flettente M (da calcolare considerando la non linearità dei materiali). Sullo stesso piano si può tracciare una retta (funzione lineare della curvatura) che rappresenta il momento totale sollecitante. Note la geometria della pila, le sue caratteristiche meccaniche e l'entità dell'azione assiale applicata, sono noti sia il diagramma momento resistente-curvatura della sezione al piede, sia la pendenza della retta degli effetti del secondo ordine M_II. E' quindi possibile tracciare molteplici rette parallele a quelle del secondo ordine che intercettano la curva momento resistente-curvatura: ciascuna di queste rette rappresenta una differente intersezione sull'asse delle ordinate, ovvero un differente momento flettente del primo ordine. Tra tutte le soluzioni ottenute è possibile calcolare direttamente il momento massimo sollecitante di progetto sopportabile della pila sotto l'assegnata azione assiale di progetto P. Se il momento sollecitante di progetto agente sulla pila è minore o uguale al valore massimo appena definito, allora la pila in esame è stabile. Il luogo dei momenti sollecitanti massimi di progetto, al variare dell'azione assiale, dà luogo ad un diagramma di interazione ridotto, ovvero il dominio resistente della sezione al piede, una volta calcolati gli effetti del secondo ordine.

Il processo grafico appare tuttavia laborioso: esso viene normalmente svolto con l'ausilio di adeguati codici di calcolo automatico.

Metodo del carico critico euleriano

Nel metodo delle tensioni ammissibili, con l'applicazione del metodo del carico critico euleriano la verifica all'instabilità risulta soddisfatta se lo stato tensionale massimo al piede della pila, nell'ipotesi che tale sezione sia la più sollecitata con parametri di sollecitazione N ed M, soddisfa le limitazioni imposte dalla normativa italiana, quando N ed M vengono amplificati con opportuni coefficienti di maggiorazione w e C. Tali coefficienti sono funzioni della geometria della pila e del carico assiale N. In questo metodo per tenere conto degli effetti della viscosità del calcestruzzo nel tempo si adotta un modulo di elasticità fittizio, riducendo opportunamente il valore di E_c.

Verifica dell’instabilità locale

Insieme all'instabilità globale della pila è necessario verificare anche l'instabilità locale delle pareti. Queste infatti, se sono di spessore molto ridotto, possono subire l'imbozzamento, facendo perdere improvvisamente la forma della sezione trasversale.