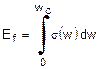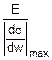MECCANICA DELLA FRATTURA E DEL DANNO - DUTTILITA' FRAGILITA' ED ENERGIA DI FRATTURA

· Meccanica dei Solidi

· Meccanica della Frattura e del Danno

· DUTTILITÁ FRAGILITÁ ED ENERGIA DI FRATTURA

· Marco Bozza

· INTRODUZIONE

· MATERIALI DUTTILI E FRAGILI

· SNERVAMENTO E INCRUDIMENTO

· ENERGIA DI FRATTURA

INTRODUZIONE

I materiali strutturali vengono tradizionalmente catalogati, in base alle caratteristiche della curva tensione-deformazione s-e, in due distinte categorie: MATERIALI DUTTILI e MATERIALI FRAGILI. Mentre i materiali duttili mostrano ampi tratti non lineari nel diaframma s-e, prima di pervenire alla rottura, quelli fragili si rompono in modo improvviso, quando la risposta è ancora sostanzialmente elastica e lineare. Una seconda caratteristica che li distingue nettamente è il rapporto tra resistenza a trazione e resistenza a compressione. Mentre per i materiali duttili tale rapporto è vicino all'unità, per i materiali fragili esso si presenta molto inferiore (in alcuni casi 10^-1 ¸ 10^-2). Le differenze di comportamento dipendono in gran parte dai meccanismi microscopici di danneggiamento e di frattura, che, nei vari materiali di impiego strutturale, si presentano notevolmente diversi.

Nelle leghe metalliche, ad esempio, si verificano degli scorrimenti tra i piani atomici e cristallini, che danno luogo ad un comportamento di tipo plastico o duttile, con notevoli deformazioni permanenti. Nei calcestruzzi e nelle rocce, d'altra parte, le microfessure e gli scollamenti tra i componenti granulari e la matrice, possono estendersi e concorrere a formare una fessura macroscopica che separa improvvisamente in due parti l'elemento strutturale. Questo processo di fessurazione instabile produce un comportamento fragile.

MATERIALI DUTTILI E FRAGILI

Peraltro non è sempre evidente quale sia l'ambito microscopico in cui avvengono i meccanismi di danneggiamento. Tale ambito può presentare dimensioni assai diverse, in funzione della natura dei meccanismi e della eterogeneità del materiale. Nei cristalli il danneggiamento avviene a livello atomico, con le vacanze e le dislocazioni; nelle leghe metalliche le cricche si propagano a livello intergranulare o transgranulare; nei calcestruzzi le fessure si enucleano all'interfaccia tra gli inerti granulari e la matrice cementizia. Si comprende quindi come la scala del danneggiamento venga a dipendere dalla regolarità del solido e quindi dalla dimensione delle eterogeneità in esso presenti.

Accanto ai materiali da costruzione tradizionali, si sono aggiunti oggi nuovi materiali, altamente eterogenei ad anisotropi, poiché rinforzati da fibre e composti da più lamine. Tali materiali, detti COMPOSITI, possono essere a matrice polimerica, metallica, ceramica o cementizia. In essi i meccanismi di danneggiamento sono essenzialmente due: lo sfilamento delle fibre e la delaminazione, cioè lo scollamento degli strati.

La distinzione tra materiali duttili e fragili non è sempre marcata in modo definito, anche perché la duttilità del materiale dipende dalla temperatura ambientale e anche dalla dimensione dell'elemento strutturale. Questo porta alla conseguenza che la duttilità cessa di essere una proprietà del materiale, per diventare una proprietà dell'intera struttura.

SNERVAMENTO E INCRUDIMENTO

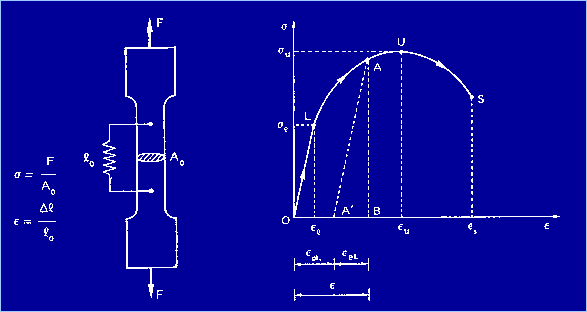
Si consideri un provino di acciaio sottoposto a una prova di trazione uniassiale di intensità F (Figura 1).

Figura 1

Per evitare che la rottura avvenga nelle zone terminali di ammorsamento alla macchina di prova, il provino abbia l'usuale forma a clessidra. Se A₀ è l'area della sezione trasversale iniziale del provino nella zona mediana ed l₀ la distanza iniziale tra due sensori fissati in due punti distinti della stessa zona, si definisce TENSIONE NOMINALE s il rapporto tra la forza F trasmessa dalla macchina e l'area iniziale A₀:

(1)

Si trascurano così le contrazioni laterali elastiche ed, eventualmente, plastiche. Si definisce poi DILATAZIONE CONVENZIONALE e il rapporto tra la variazione di distanza tra i due sensori, Dl, e la distanza l₀:

(2)

Tale dilatazione è quella media, relativamente al tratto sotto controllo. Poiché la prova si svolge in regime non lineare, la dilatazione non è uniforme, e quindi non è puntualmente coincidente con quella madia.

Si consideri il diagramma della Figura 1 riportante tutte le coppie di punti s-e registrati durante il processo di caricamento. Si vede che il tratto OL è lineare ed elastico, mentre da L in poi la risposta non è più lineare ed il materiale comincia a snervarsi. Scaricando il provino si evidenziano le deformazioni permanenti e_pl. In questo modo parte dell'energia di deformazione è restituita (triangolo ABA'), cioè quella relativa alla deformazione e_el, mentre la restante è dissipata plasticamente (area OLAA'). Caricando nuovamente il provino, si ripercorre elasticamente il tratto A'A, parallelo al tratto OL. Giunti in A, il provino si snerva di nuovo ad una tensione s > s_l. Il materiale vergine, quindi, si snerva a livelli di tensione più bassi di quanto non faccia il materiale già precedentemente snervato. Questo fenomeno è detto INCRUDIMENTO del materiale (HARDENING). Aumentando la forza applicata F, si riprende a percorrere il tratto non lineare AU, nel quale l'incremento di tensione per incremento unitario di dilatazione (RIGIDEZZA TANGENZIALE) continua a diminuire, finché non si annulla nel punto U. Giunti in U, se il processo di caricamento è pilotato dalla forza esterna F, il provino si rompe, poiché F non può aumentare ulteriormente.

Se, invece, il processo di caricamento è pilotato dalla variazione di distanza Dl, è possibile indagare sul comportamento del materiale al là del punto U di resistenza ultima. Oltre il punto U, infatti, la rigidezza tangenziale diventa negativa e, ad incrementi positivi di spostamento Dl, corrispondono incrementi negativi della forza F (la forza diminuisce lungo il tratto US). Ciò è dovuto al fenomeno della CONTRAZIONE TRASVERSALE PLASTICA, detta anche STRIZIONE (Figura 2), per cui l'area A della sezione effettiva diventa notevolmente inferiore di A₀, in una banda localizzata compresa tra i due sensori.

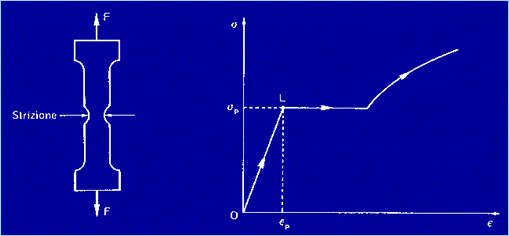
Figura 2

Infine, raggiunto il punto terminale S, il provino cede improvvisamente, sebbene il processo di caricamento sia a deformazione controllata.

Nel caso di alcune leghe metalliche, come gli acciai a basso contenuto di carbonio, al limite di proporzionalità L segue uno snervamento improvviso, con la conseguenza che la dilatazione aumenta di una quantità finita sotto carico costante (si veda il diagramma s-e della Figura 2).

In questi casi è quindi facile individuare il valore della TENSIONE DI SNERVAMENTO ASSIALE s_p, essendo questa coincidente con il limite di proporzionalità s_l. Quando, invece, al limite di proporzionalità segue il tratto incrudente, è più difficile definire s_p: si adotta, allora, per convenzione, quel valore della tensione la cui dilatazione permanente e_pl allo scarico è pari al 2 %_o.

Mentre i materiali duttili presentano comportamenti simili a trazione e compressione, i materiali fragili mostrano comportamenti considerevolmente differenti. I calcestruzzi, ad esempio, sono duttili in compressione e fragili in trazione, e presentano una resistenza ultima a compressione che è circa di un ordine di grandezza maggiore di quella a trazione. Una prova di trazione su di un campione di calcestruzzo, condotta a carico controllato, mostra una risposta approssimativamente elastica-lineare e poi, all'improvviso, una immediata caduta del carico stesso, che corrisponde alla repentina formazione di una fessura. Tuttavia, poiché le attuali tecniche consentono di pilotare la deformazione, si evidenzia la curva di risposta post-rottura del materiale cementizio (Figura 3).

Figura 3

Ci si è resi così conto dell'esistenza di un esteso ramo di INCRUDIMENTO NEGATIVO (SOFTENING) e della possibilità di dissipare, da parte del materiale, una notevole quantità di energia per unità di volume. Tale energia è rappresentata dall'area sottesa dalla curva s(e). Di recente si è dimostrato che l'energia in realtà non è dissipata per unità di volume, bensì è dissipata su una banda localizzata, la quale diventa in seguito una fessura (l'analogo fenomeno avviene nei materiali duttili con la strizione). 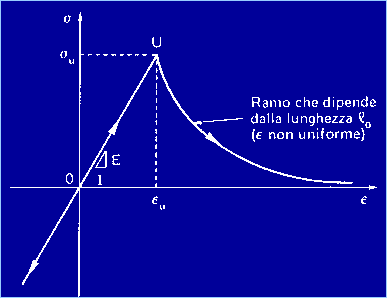In altri termini, la dilatazione puntuale tra i due sensori di Figura 1 non è una funzione costante. In conseguenza della localizzazione della deformazione e, il ramo decrescente s(e) viene a dipendere dalla lunghezza l₀ della base di misura.

ENERGIA DI FRATTURA

Ciò che invece risulta essere una vera caratteristica del materiale è il diagramma s(w), che rappresenta la tensione trasmessa attraverso la fessura, in funzione dell'apertura (o larghezza) della fessura stessa (Figura 4).

Figura 4

Questa legge di decadimento indica un indebolimento dell'interazione all'aumentare della distanza w tra le facce (o superfici libere) della fessura. Quando w raggiunge il valore limite w_c, l'interazione si spegne totalmente e la fessura diventa una sconnessione completa che divide in due parti distinte il provino. L'area sottesa dalla curva s(w) rappresenta l'energia dissipata sulla superficie unitaria di frattura. Essendo la legge coesiva s(w) una caratteristica del materiale, che dipende dalla struttura intima e dai meccanismi di danneggiamento del materiale stesso, anche l'ENERGIA DI FRATTURA E_f, definita da:

(3)

risulta essere una proprietà intrinseca del materiale. L'energia dissipata sulla superficie della fessura vale E_fA₀. Poiché, tuttavia, si è supposto che la dissipazione energetica avvenga soltanto sulla superficie fessurata, e non nel volume di materiale integro, l'energia dissipata globalmente nel volume A₀l₀ è ancora pari a E_fA₀ (questo però è rigorosamente vero solo in assenza di incrudimento positivo).

Figura 5

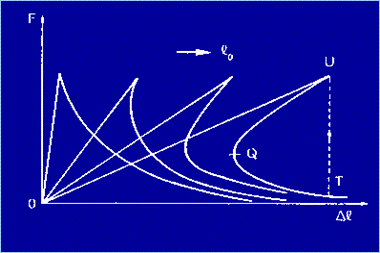
Figura 6

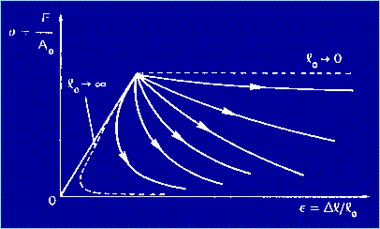
Se si riportano allora le curve di risposta sul piano F-Dl si ottiene il grafico della Figura 5. Da esso si vede che all'aumentare della lunghezza l₀ del provino, si ottengono tratti elastici a rigidezza calante e tratti "softening" a pendenza negativa crescente e, oltre un cero limite, a pendenza positiva. L'area sottesa da ciascuna curva deve infatti essere costante e pari a E_fA₀.

Se si riporta sul piano s-e la transizione appena descritta si ottengono le curve della Figura 6. Questo grafico è rappresentato da un unico tratto elastico lineare e da un ventaglio di rami "softening", al variare della lunghezza l₀. L'area sottesa, infatti, in questo caso varia con l₀, essendo pari a E_f/l₀. Per l₀ ® 0 il ramo "softening" diventa orizzontale e rappresenta una risposta strutturale perfettamente plastica. D'altra parte, per l₀ ® ¥ l'area compresa tra la curva s(e) e l'asse e deve tendere a zero, e quindi il ramo "softening" tende a coincidere con il tratto elastico. Si può dimostrare che si hanno tratti "softening" a pendenza positiva quando è verificata la relazione seguente:

(4)

l₀ >

cioè, quando la lunghezza del provino, o meglio la distanza l₀ tra i punti di cui si stima lo spostamento relativo, è superiore al rapporto tra il modulo elastico E del materiale e il massimo modulo tangente della legge coesiva. Questo è dovuto al fatto che, durante la fase di incrudimento negativo, la tensione s diminuisce e, mentre il punto rappresentativo della zona fessurata scende lungo la curva s(w) (Figura 4), il punto rappresentativo della zona integra scende lungo la retta s(e) (Figura 3) e descrive uno scaricamento elastico. Se la lunghezza l₀ è sufficientemente grande, la contrazione elastica prevale sulla dilatazione della zona fessurata, dando luogo al fenomeno precedentemente descritto.

Se il processo di carico è pilotato dalla dilatazione convenzionale e, o dall'allungamento Dl, una volta raggiunto il punto U (Figura 5), si ha una caduta verticale del carico, sino ad incontrare il tratto "softening" inferiore che è a pendenza negativa. Il tratto UQT viene in questo modo ignorato e diventa virtuale. Per rilevare sperimentalmente questo tratto, è necessario pilotare il processo di carico mediante l'apertura w della fessura. L'instabilità sopra descritta è detta SNAP-BACK. Tutti i materiali relativamente fragili (calcestruzzo, ghisa, vetro,…), che possiedono un basso valore dell'energia di frattura E_f presentano una brusca caduta del carico quando il comportamento globale del campione è ancora elastico lineare.

Riassumendo quanto detto è opportuno osservare come resistenza ed energia di frattura siano proprietà intrinseche del materiale, mentre la duttilità dipenda da un fattore strutturale come la lunghezza del campione.