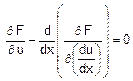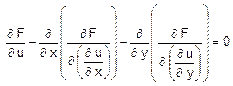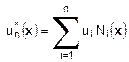· Meccanica Computazionale

· Metodo degli Elementi Finiti: Teoria Matematica

· FORMULAZIONE VARIAZIONALE E RESIDUALE

· Marco Bozza

· INTRODUZIONE

· EQUAZIONE DI EULERO

· VANTAGGI DELLA FORMULAZIONE VARIAZIONALE

· DEDUZIONE DI PRINCIPI VARIAZIONALI

· METODO VARIAZIONALE DI RAYLEIGH-RITZ

· METODO VARIAZIONALE DI GALERKIN

· METODO VARIAZIONALE DEI RESIDUI PESATI

INTRODUZIONE

La soluzione di un problema mediante discretizzazione agli elementi finiti è strettamente connessa al concetto di Formulazione Variazionale. Storicamente lo sviluppo della formulazione variazionale dei problemi fisici nacque dalla scoperta fatta da Eulero nel 1744 del Principio di Minima Azione. Secondo tale principio tutti i fenomeni che avvengono in natura rispettano metodi ai valori estremi. Come conseguenza furono ricavate le equazioni della dinamica tramite Lagrange (1788) ed Hamilton (1834).

Per formulazione variazionale di un problema fisico stazionario si intende la trasformazione in forma integrale delle equazioni differenziali che lo regolano. Più precisamente, esiste un principio variazionale alla base di un fenomeno fisico quando la soluzione del problema matematico che lo descrive è riconducibile alla ricerca di un funzionale che renda estrema una espressione integrale. Tale funzione appartiene ad una classe di funzioni ammissibili, soddisfacenti determinati requisiti di regolarità e determinate condizioni al contorno.

EQUAZIONE DI EULERO

Funzionale

L'espressione matematica di un principio variazionale, cioè la sua espressione integrale, che è una funzione di funzioni, si chiama funzionale e lo indichiamo conF. Supponendo che il problema sia descritto dalla funzione F della variabile indipendente u(x), funzione a sua volta della sola variabile x nel dominio G, e delle sue derivate, il funzionale assume la seguente definizione generale:

(1)

mentre se la funzione u(x,y) dipende da due variabili nel dominio di integrazione W, il funzionale diventa:

(2)

In queste ipotesi il funzionale assume un preciso significato fisico. Una volta che sia stato individuato tale integrale, il Calcolo Variazionale si propone di studiare la condizione di stazionarietà (minimo, massimo, flesso), ovvero di determinare, fra tutte le funzioni ammissibili u quella funzione particolare u^* che estremizza, ossia minimizza o massimizza, il funzionale stesso. In altre parole, lo scopo del calcolo variazionale non è quello di trovare i valori che rendono estremi una funzione in un numero finito di variabili, ma quello di trovare nel gruppo di funzioni ammissibili la funzione che rende stazionario un dato funzionale.

Equazione di Eulero

Si dimostra che la condizione necessaria (ma non sempre sufficiente) per l'esistenza di un valore estremo è che esista l’equazione di Eulero associato al problema stazionario, nel senso che la funzione estremizzante deve necessariamente soddisfare l'equazione di Eulero associata al funzionale F. Nel caso particolare che il funzionale abbia la forma:

(3)

la condizione necessaria perché u^* sia soluzione del problema variazionale (renda estremo il funzionale) è che soddisfi l’equazione di Eulero:

(4)

mentre per:

(5)

l’equazione di Eulero vale:

(6)

Altre volte si ricorre, invece, ad un principio variazionale per risolvere un’equazione differenziale: è il caso che si incontra in Ingegneria o Fisica. In questa ipotesi il problema fisico è descritto da una PDE e si va a cercare il funzionale (se esiste) la cui equazione di Eulero coincide con l’equazione originale. Può accadere allora che il funzionale trovato non abbia un significato fisico. Si dimostra anche che imponendo la condizione di stazionarietà del funzionale automaticamente viene soddisfatta l'equazione differenziale di Eulero insieme alle relative condizioni naturali. Questo porta alla conclusione che la soluzione della PDE (e delle sue condizioni naturali) del problema stazionario è equivalente alla condizione di stazionarietà del funzionale. Quindi anziché risolvere l'equazione differenziale, si può cercare la condizione di stazionarietà del funzionale ad essa associato.

VANTAGGI DELLA FORMULAZIONE VARIAZIONALE

La meccanica del continuo è uno dei campi della fisica matematica dove la tecnica variazionale è stata oggetto di approfondita ricerca. Per questi problemi il funzionale è rappresentato dall'energia potenziale, il cui valore deve essere stazionario e minimo affinché il sistema sia in equilibrio stabile. I vantaggi della formulazione variazionale sono:

- invarianza del funzionale per trasformazioni di coordinate (questo per il significato fisico dei suoi parametri);

- la trasformazione di un dato problema in uno equivalente risolubile più facilmente di quello originale;

- le condizioni al contorno naturali sono già comprese nel funzionale;

- se l'equazione differenziale ha ordine 2m, il funzionale ha ordine m.

Il problema che ora si pone è come passare dalla PDE al funzionale per problemi stazionari. Questa trasformazione, quando è possibile, può essere fatta o in modo rigoroso, oppure utilizzando il significato fisico del funzionale. Come già detto, una volta costruito il funzionale associato alla PDE, si procede ad applicarlo rigorosamente imponendo la condizione di minimo del funzionale all’insieme continuo.

DEDUZIONE DI PRINCIPI VARIAZIONALI

Come detto un principio variazionale può essere formulato direttamente oppure sulla base della conoscenza della sua equazione di Eulero. A volte l’equazione che si vuole risolvere non è un’equazione di Eulero e pertanto non esiste il principio variazionale ad essa associato. Anche quando esiste, non c’è una regola generale per ricavarlo: spesso occorre procedere per tentativi. Esistono tuttavia dei criteri che consentono di darci delle indicazioni circa l’esistenza e la deducibilità di principi variazionali associate alle PDE.

Supponiamo che il problema sia descritto nello spazio 3D dalle seguenti equazioni:

(7)
(8)

dove A e G sono operatori differenziali lineari sul dominio di integrazione G e sul contorno, rispettivamente, ed f sia una funzione continua di x. Si dimostra allora che un principio variazionale corrispondente a queste equazioni esiste solo se l’operatore A è auto-aggiunto e definito positivo. Si ricorda che un operatore A si definisce auto-aggiunto (o simmetrico) se:

(9)

per ogni coppia di funzioni u(x) e v(x) che soddisfano le condizioni al contorno omogenee del problema dato. Inoltre un operatore auto-aggiunto A è anche definito positivo se:

(10)

per tutte le funzioni u(x) che soddisfano le condizioni al contorno omogenee. Nelle ipotesi precedenti si dimostra che la funzione u(x) rende estremo il funzionale:

(11)

per cui la (11) è il funzionale associato all’equazione (7) per operatore A auto-aggiunto e definito positivo, e funzione u(x) soddisfacente le condizioni al contorno (8). Nel caso di problemi con condizioni al contorno non omogenee l’espressione del funzionale assume una formulazione più complicata in dipendenza del problema considerato.

METODO VARIAZIONALE DI RAYLEIGH-RITZ

Si è visto che nel, caso di problemi stazionari, una PDE si può trasformare con l’ausilio del calcolo variazionale in una equazione integrale (funzionale). Se inoltre l’equazione ha la forma della (7) con condizioni al contorno (8), e se l’operatore A è auto-aggiunto e definito positivo, il funzionale F(u) associato è dato dalla (11). Per risolvere l’equazione differenziale si può utilizzare un procedimento approssimato noto come Metodo di Rayleigh-Ritz. Il principio su cui si basa il metodo è il seguente: se u* è la funzione che minimizza il funzionale F(u), e se questa è definita in un sottospazio finito S_n di dimensione n dello spazio funzionale lineare S della soluzione, una soluzione approssimata u_n* appartenente a S_n può esprimersi nella forma:

(12)

La (12) è una combinazione di funzioni note N_i(x), dette Funzioni di Forma, e parametri incogniti u_i detti coefficienti di Ritz. Le funzioni N_i(x) sono scelte in maniera tale da rispettare le condizioni essenziali nell’intero dominio del sistema. Esse devono definire una base completa e linearmente indipendente, e sono l’analogo dei vettori base in uno spazio vettoriale n-dimensionale. In questo modo se u_n* minimizza F(u), F(u_n*) è vicino a F(u*) e u_n* sarà prossimo a u*. Per calcolare i parametri u_i si minimizza F(u_n*), derivando F rispetto a questi coefficienti, ottenendo le n equazioni di Ritz:

(13)

Nell’ipotesi di funzionale quadratico la (13) rappresenta un sistema di n equazioni lineari la cui soluzione fornisce il vettore dei coefficienti di Ritz, e quindi la soluzione approssimata cercata.

METODO VARIAZIONALE DI GALERKIN

Il Metodo di Galerkin costituisce una generalizzazione di quello di Rayleigh-Ritz, in quanto permette di risolvere in modo approssimato l’equazione (7) anche se l’operatore differenziale A è non lineare e anche non auto-aggiunto. In queste ipotesi, esprimendo ancora la soluzione approssimata u_n(x) nella forma (12), si definisce residuo la quantità:

(14)

Esso si annulla solamente per u_n(x)=u(x). Nel metodo di Galerkin i parametri u_i (chiamati ora coefficienti di Galerkin) vengono determinati risolvendo gli n integrali variazionali di Galerkin:

(15)

Nella (15) le funzioni N_i(x) devono ancora soddisfare le condizioni (8). L’interpretazione geometrica della (15) è la seguente: nel caso generale che la (14) rappresenti una relazione vettoriale nello spazio 3D (le funzioni N_i(x) diventano i vettori linearmente indipendenti della base), il residuo è il vettore differenza tra il vettore approssimato f_n(x)=Au_n(x) ed il vettore (esatto) f(x). L’intensità di r_n(x) rappresenta anche la distanza tra gli estremi dei due vettori. Questa distanza (errore) è minima quando il vettore residuo r_n(x) è ortogonale simultaneamente ai 3 vettori N_i(x) della base che definiscono la soluzione approssimata. In sostanza, i coefficienti di Galerkin u_i sono determinati risolvendo le n equazioni (15), con le quali viene imposta l’ortogonalità tra il residuo e le n funzioni di forma N_i(x) (si noti tuttavia che nel caso di uno spazio 3D un vettore può essere contemporaneamente perpendicolare a 3 vettori linearmente indipendenti solo per r₃(x)=0).

Con questo metodo le (15) non scaturiscono più dalla minimizzazione di un funzionale, per cui non è più necessario che l’operatore A possieda le proprietà di linearità e simmetria. Ne segue che esse sono più generali delle equazioni di Ritz, e possono essere usate per risolvere qualsiasi equazione differenziale (è questo il vantaggio del metodo di Galerkin nel FEM!). Il metodo di Galerkin converge alla soluzione esatta al crescere di n, anche se non esiste un funzionale associato per il quale u_n(x) debba essere soluzione di minimo.

METODO VARIAZIONALE DEI RESIDUI PESATI

Si è visto che il metodo variazionale di Galerkin è una generalizzazione di quello di Rayleigh-Ritz, col quale coincide quando le equazioni differenziali da risolvere del tipo (7) hanno operatore A auto-aggiunto e lineare. A sua volta il metodo di Galerkin è un caso particolare del più generale Metodo Variazionale dei Residui Pesati. Questo metodo impone l’ortogonalità tra il residuo r_n(x) ed una base di funzioni W_i(x), dette funzioni peso, diversa da quella usata per approssimare la soluzione. L’equazione del metodo dei residui pesati è pertanto:

(16)

Se la base W_i(x) è completa e linearmente indipendente la soluzione tende alla soluzione esatta, mentre il residuo converge al valore nullo. L’equazione (16) coincide con l’equazione di Galerkin (15) quando W_i(x)=N_i(x).

A seconda della scelta delle funzioni peso il metodo dei residui pesati assume diverse denominazioni:

- metodo di Galerkin

- metodo dei sottodomini

- metodo di collocation

- metodo dei minimi quadrati

- metodo dei momenti

Tuttavia il metodo di Galerkin è, tra tutti i metodi dei residui pesati, quello più comunemente impiegato con il FEM. Tutti questi metodi hanno il grande vantaggio di prescindere dalla conoscenza del funzionale F. Quando una PDE ammette un principio variazionale, esso è sempre equivalente ad un metodo dei residui pesati. L’inverso non è vero, poiché i metodi dei residui pesati sono applicati direttamente al problema differenziale, indipendentemente dall’esistenza o meno del funzionale associato.