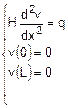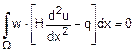METODO DEGLI ELEMENTI FINITI - FORMULAZIONE DEL PROBLEMA STRUTTURALE

· Meccanica Computazionale

· Metodo degli Elementi Finiti: Teoria Matematica

· FORMULAZIONE DEL PROBLEMA STRUTTURALE

· Andrea Bacchetto

· INTRODUZIONE

· FORMULAZIONI DEL PROBLEMA STRUTTURALE

· IL PRINCIPIO DEI LAVORI VIRTUALI

INTRODUZIONE

Dagli studi che generalmente si seguono ai corsi di ingegneria si è abituati a fare un’analisi a livello dell’elemento infinitesimo del corpo oggetto di studio. L’applicazione delle relative equazioni di equilibrio, costitutive e di conservazione permettono di ottenere delle equazioni differenziali che governano il comportamento del sistema a livello infinitesimo. Tali relazioni così ricavate presentano spesso una forma piuttosto complicata e, nella maggior parte dei casi pratici, non sono risolvibili in forma chiusa (cioè esatta) a causa di articolate condizioni al contorno ed alla non regolarità del dominio di integrazione.

La soluzione di un qualsiasi problema governato da note equazioni differenziali può essere affrontata in tre differenti modalità, ognuna delle quali presenta diverse caratteristiche e particolarità.

Un problema strutturale può essere riportato in una delle seguenti forme: la formulazione forte, la formulazione debole e la formulazione variazionale.

Tra queste quelle debole e variazionale sono direttamente collegate al FEM: le equazioni differenziali vengono trasformate in equazioni algebriche, mediante operazioni di integrazione o di derivazione. L’insieme delle equazioni algebriche è sistematicamente risolvibile mediante la teoria dei sistemi lineari.

FORMULAZIONI DEL PROBLEMA STRUTTURALE

Formulazione forte

La formulazione di un problema in base alle sue equazioni differenziali, unite alle necessarie condizioni al contorno, è la cosiddetta formulazione forte, di cui è possibile valutare la soluzione analitica (quindi esatta) solo per un certo numero limitato di casi particolari: semplici condizioni al contorno ed un dominio di integrazione regolare. Si consideri ad esempio l’equazione differenziale che governa il problema della fune inestensibile:

(1)

dove v(x) è lo spostamento verticale, H è il tiro della fune, x è l’ascissa e q è il carico distribuito che agisce sulla fune. Si ponga l’attenzione sul fatto che se viene definito l’operatore differenziale come segue:

(2)

il problema rappresentato dalla (1) può quindi essere riscritto nella forma:

(3)

Tale forma di rappresentare il problema in forma forte è tipica della teoria degli operatori dove nella (3) si può leggere come un’applicazione lineare da uno spazio vettoriale delle forze ad un altro degli spostamenti:

(4)

Formulazione debole

A causa delle già citate complicazioni legate alla soluzione analitica delle equazioni differenziali, si cerca di risolvere tali problemi mediante l’impostazione della formulazione debole. Il problema impostato secondo la formulazione forte viene trasformato al fine di diminuire il grado di derivazione delle equazioni.

Consideriamo ad esempio lo stesso problema del punto precedente; si proceda al calcolo del residuo ponderato mediante le funzioni peso w e quindi integrando su tutto il dominio W:

(5)

La principale caratteristica delle formulazioni deboli è quindi la possibilità di diminuire il grado di derivazione delle equazioni differenziali (indebolendole appunto) mediante una procedura matematica che consiste nell’integrazioni per parti. Dalla (5) si può inoltre evincere come tale impostazione consideri il residuo dell’equazione differenziale eventualmente approssimata. In particolare il residuo viene valutato su tutto il dominio rendendo meno restrittiva la richiesta (valore medio e non puntuale).

Formulazione variazionale

Con la formulazione variazionale si caratterizza la soluzione mediante un metodo matematico che permetterà di costruire le equazioni equilibrio come estremanti di un funzionale, dove per funzionale si intende un’applicazione P (ad esempio potenziale totale del sistema) del tipo:

(6)

essendo X uno spazio vettoriale e Â l’insieme dei numeri reali.

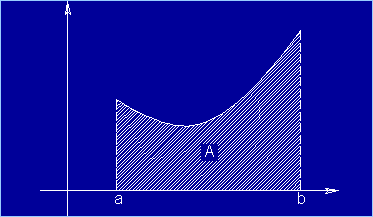
L’impostazione variazionale nasce dalla considerazione che ogni fenomeno fisico viene retto da una qualche grandezza (ad esempio il funzionale) che, per trovare una condizione di equilibrio, deve essere resa massima o minima. Si pensi ad esempio alla catenaria dove tra le possibili configurazioni di equilibrio, quella che si verifica in natura è quella che realizza la minima area A racchiusa alla catena stessa e da un asse di riferimento (vedi Figura 1).

Figura 1

L’equazione algebrica tipo si costruirà mediante una procedure di derivazione simile alla seguente:

(7)

Il vantaggio di una formulazione variazionale sta nel fatto che le equazioni che se ne ricavano contengono già all’interno le condizioni naturali (di Neumann). Ad esempio le forze interne che nel metodo diretto vengono considerate, in quello variazionale non vengono prese in considerazione perché compiono lavoro nullo.

Un altro vantaggio della formulazione variazionale, oltre che nella possibilità di ricavare le equazioni algebriche con metodi sistematici, sta anche nel fatto che le condizioni al contorno naturali (di Neumann) sono già contenute all’interno del funzionale. Per contro il procedimento non permette un diretto controllo sulle equazioni generate in quanto non sono facilmente riconducibili relazioni con il mondo fisico ed inoltre non è sempre facile riuscire a ricavare il funzionale del problema in esame.

IL PRINCIPIO DEI LAVORI VIRTUALI

Uno dei principi più utilizzati per lo sviluppo della teoria degli elementi finiti risulta essere il principio dei lavori virtuali (PLV), che afferma:

“L’applicazione di uno spostamento virtuale congruente con le condizioni di vincolo ad un sistema in equilibrio, genera un sistema di forze (interne, esterne e vincolari) tale per cui il lavoro interno (quello prodotto dalle forze interne) risulta uguale al lavoro esterno (quello prodotto dalle forze esterne)”

Come è noto il lavoro di una forza è pari al prodotto scalare della forza per lo spostamento del suo punto di applicazione. Il lavoro virtuale sfrutta la stessa definizione:

(8)

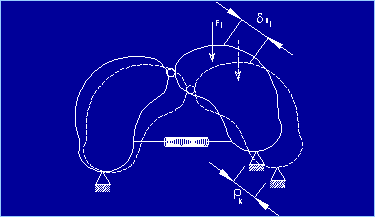
Con riferimento alla Figura 2 è possibile scrivere il principio dei lavori virtuali come segue:

(9)

dove du_i sono gli spostamenti dei punti di applicazione delle forze, r_j sono i cedimenti vincolari e ds_k sono gli spostamenti virtuali interni (allungamento della molla).

Figura 2

Tale principio è uno strumento molto potente per poter ricavare le relazioni matriciali che servono per l’implementazione in codici di calcolo in grado di risolvere le strutture idealizzate.

Uso e riferimento per un utilizzo generale trova una vasta applicazione in molti campi. Inoltre, non avendo formulato nessuna ipotesi sulla natura delle leggi costitutive, queste possono essere lineari o non-lineari. Le ipotesi che devono essere rispettate sono:

· la congruenza tra spostamenti e deformazioni;

· l’equilibrio tra forze interne, esterne e vincolari.

La potenza del principio è insita nella possibilità di scindere i due sistemi: forze e spostamenti - deformazioni non devono essere necessariamente legati l’uno all’altro. Ciò significa che una struttura può essere studiata nel suo comportamento usando delle forze di prova, ottenendo come risultato un campo degli spostamenti che rappresenterà, per l’appunto, il comportamento.