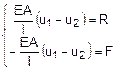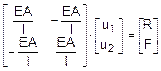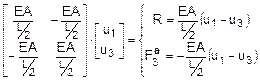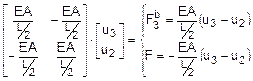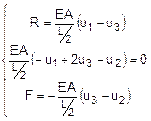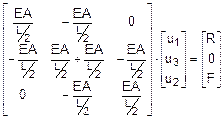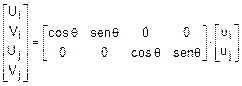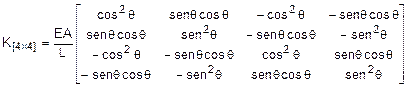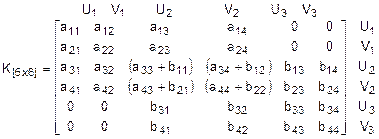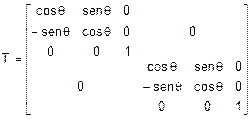METODO DEGLI ELEMENTI FINITI - ASSEMBLAGGIO DEGLI ELEMENTI FINITI

· Meccanica Computazionale

· Metodo degli Elementi Finiti: Modellazione

· ASSEMBLAGGIO DEGLI ELEMENTI FINITI

· Andrea Bacchetto

· INTRODUZIONE

· SEMPLICE ESEMPIO DI ASSEMBLAGGIO

· ASSEMBLAGGIO DI ELEMENTI FINITI MONODIMENSIONALI

· I TELAI PIANI: PRIMI ESEMPI DI DISCRETIZZAZIONE

· ASSEMBLAGGIO DI ELEMENTI FINITI BIDIMENSIONALI

INTRODUZIONE

La soluzione delle equazioni differenziali che governano un problema strutturale, mediante la formulazione debole dello problema stesso, viene ricondotta alla soluzione di una serie di equazioni algebriche. Questo è permesso dalla discretizzazione della struttura tramite una mesh (maglia) di elementi finiti. Tali equazioni, opportunamente ordinate in un sistema lineare, in scrittura matriciale, possono essere raggruppate nella forma seguente:

(1)

dove K è la matrice globale di rigidezza del sistema, u è il vettore degli spostamenti (incognita del problema) ed f è il vettore delle forze applicate (termine noto del problema).

Figura 1

L’integrazione delle relazioni differenziali sui sottodomini (W_i) individuati dai singoli elementi finiti (Figura 1) permette di valutare le matrici (di massa, di rigidezza, ecc.) per ognuno di questi elementi. La soluzione del problema deve necessariamente utilizzare uno strumento che riesca a trattare tutte le singole matrici come un’unica matrice del sistema. È quindi indispensabile eseguire un’operazione di assemblaggio.

SEMPLICE ESEMPIO DI ASSEMBLAGGIO

Assemblaggio : il complesso delle operazioni necessarie per mettere insieme le varie parti precostituite, di macchinari, apparecchi o manufatti, talora anche figure.

Dalla definizione sopra riportata si evince che il processo di assemblaggio prevede, una volta creati i singoli oggetti (matrici degli elementi), la formazione di un unico pezzo (matrice globale), mediante un’opportuna operazione di assemblaggio.

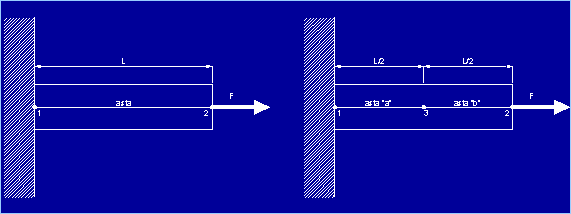
Per comprendere cosa significa assemblare le matrici degli elementi finiti, inizieremo considerando l’esempio descritto nelle figure sottostanti. Modelliamo un’asta agente solo a sforzo normale (per la quale l’unico grado di libertà coinvolto è quello alla traslazione orizzontale) in due differenti modelli:

- modello tipo A con una sola asta (Figura 2, sinistra);

- modello tipo B con due aste (Figura 2, destra).

Figura 2

Per il modello tipo A valgono le seguenti relazioni di equilibrio rispettivamente al nodo 1 ed al nodo 2:

(2)

dove EA/L è la rigidezza assiale dell’elemento e R è la reazione vincolare al nodo 1. In forma matriciale il sistema (2) può essere riscritto nella forma seguente:

(3)

Per il modello tipo B, dove i due elementi usati per la modellazione dell’asta hanno una lunghezza pari alla metà di quella dell’asta stessa, si rende necessario scrivere un set di relazioni di equilibrio per ognuno degli elementi.

Per l’asta “a” valgono le seguenti relazioni che forniscono i valori delle forze ai nodi 1 e 3:

(4)

Per l’asta “b” valgono le seguenti relazioni che forniscono i valori delle forze ai nodi 3 e 2:

(5)

L’equilibrio del nodo 3 deve essere assicurato mediante l’imposizione dell’uguaglianza delle forze che nascono al nodo 3 considerato appartenente sia all’asta “a” che all’asta “b”. La relazione di equilibrio di tale forze viene impostata come segue:

(6)

La scrittura del sistema che descrive il modello tipo B risulta quindi il seguente:

(7)

La scrittura matriciale del sistema (7) si presenta nella seguente forma:

(8)

OSSERVAZIONE 1: I termini corrispondenti ad elementi diversi, ma contribuenti allo stesso nodo (termini riquadrati in (8)), vengono semplicemente sommati nel corrispondente termine della matrice globale.

OSSERVAZIONE 2: i termini in posizione ij nulli della matrice sono da interpretare come una non interferenza tra la forza applicata al nodo j e lo spostamento del nodo i.

In generale si può affermare che l’operazione di assemblaggio prevede che i gradi di libertà locali (appartenenti all’elemento) che contribuiscano allo stesso grado di libertà globale (dell’intero modello), vengano opportunamente sommati, costituendo un unico valore all’interno della matrice globale.

ASSEMBLAGGIO DI ELEMENTI FINITI MONODIMENSIONALI

Con l’esempio precedente si è cercato di chiarire in maniera diretta il significato di assemblaggio di due elementi finiti.

Con l’esempio che viene proposto nel seguito si eseguirà una nuova operazione di assemblaggio introducendo la matrice di rotazione. Tale matrice permetterà di trasformare il sistema di riferimento locale dell’elemento in quello globale.

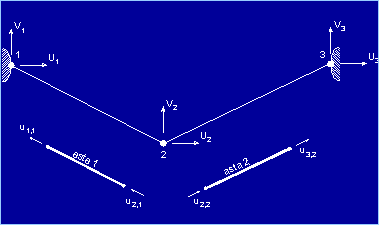
Si noti che la struttura proposta non è caricata, focalizzeremo infatti l’attenzione al solo assemblaggio delle matrici di rigidezza. L’estensione a matrici e vettori coinvolti nell’analisi strutturale seguiranno gli stessi principi.

Osservando le due aste di tipo truss riportate nella Figura 3, è facile intuire che:

- il grado di libertà locale u_1,1 contribuisce ai gradi di libertà globali u₁ e v₁.

- i gradi di libertà locali u_2,1 e u_2,2 contribuiscono a quelli globali u₂ e v₂.

- il grado di libertà locale u_3,2 contribuisce ai gradi di libertà globali u₃ e v₃.

Figura 3

Prima di eseguire la valutazione della matrice globale, risulta necessario trasformare le matrici delle singole aste (valutate in un riferimento locale) riportando i singoli contributi in riferimento comune (quello globale). Tale operazione si attua mediante matrici di rotazione che permettono la trasformazione da un sistema di gradi di libertà locale a quello globale attraverso una semplice rotazione di assi.

Per i truss evidenziati in figura la matrice di rotazione permette di passare da un sistema ad un grado di libertà per ogni nodo ad un riferimento cui sono attivi due gradi di libertà.

(9)

dove q rappresenta la rotazione del sistema locale rispetto a quello globale, attorno all’asse uscente dal piano della rappresentazione del modello. L’operazione di trasformazione prevede una pre- e post-moltiplicazione delle matrici di rigidezza locali con quella di rotazione riportata in (9):

(10)

dove K*_[2x2] è la matrice del sistema (3). È interessante notare come la matrice di rigidezza di un singolo elemento passa da una dimensione pari a due ad una dimensione pari a quattro: per ogni nodo infatti ci sono due gradi di libertà globali; a livello dell’elemento asta i gradi di libertà diventano quindi quattro.

Eseguendo i prodotti in (10) si ottiene la seguente matrice:

(11)

La matrice in (11) è quindi la matrice di rigidezza di un elemento truss riportata nel sistema di riferimento globale. È ora possibile proseguire con l’operazione di assemblaggio. Riferendoci alla Figura 3 andremo ad individuare l’angolo dell’asta 1 con a e quello relativo all’asta 2 con b. Ne risulteranno due matrici che per semplicità di esposizione le indicheremo con A e B:

(12)

La creazione della matrice globale, che presenta una dimensione pari al numero di gradi di libertà cui gode il sistema rappresentato in Figura 3, viene effettuata coma segue:

(13)

OSSERVAZIONE 3: La possibilità di costruire la matrice di ogni elemento e successivamente di assemblarle in quella globale permette di poter modellare strutture composte da elementi caratterizzati da proprietà fisico-meccaniche diverse. Tale aspetto è uno dei punti di forza, in base al quale il FEM si è imposto come mezzo di indagine sperimentale e di progetto.

OSSERVAZIONE 4: L’operazione di assemblaggio è fondamentale per costruire le matrici globali della struttura: se la struttura è in campo statico verrà formata solo quella di rigidezza; se invece la struttura è in campo dinamico anche quelle di massa e di viscosità.

OSSERVAZIONE 5: Per eseguire l’assemblaggio delle matrici degli elementi è necessario “mappare” tutti i gradi di libertà della struttura secondo una numerazione globale e quindi univoca. A seguito dell’assegnazione di tale ordine, si faranno corrispondere i gradi di libertà locali a quelli globali.

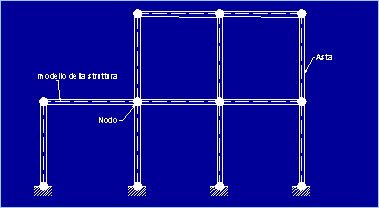
I TELAI PIANI: PRIMI ESEMPI DI DISCRETIZZAZIONE

Storicamente la prima idealizzazione delle strutture è quella degli edifici civili, per i quali una discretizzazione ad elementi beam (elementi trave soggetti a sforzo normale, flessione e taglio; sviluppati secondo la classica teoria della trave) o truss (ideali per le modellazioni di strutture reticolari) è stata largamente utilizzata.

Per una struttura a telaio o per una reticolare l’elemento finito di base è il modello asta, che schematizza le varie membrature (pilastri e travi) con elementi monodimensionali i cui nodi coincidono con i nodi strutturali di collegamento tra travi e pilastri (Figura 4).

Figura 4

La matrice di rigidezza per un’asta sollecitata nel piano a taglio, sforzo normale e momento flettente è riportata in (14). Si noti come tale matrice sia un’estensione di quella usata negli esempi precedenti dove l’unico grado di libertà attivo risultava quella alla traslazione assiale.

(14)

La matrice (14) viene ricavata mediante l’applicazione di distorsioni (traslazioni e rotazioni) unitarie applicate alternativamente ai nodi. Tale matrice si riferisce infatti ad un vettore nelle incognite ordinate come segue:

(15)

dove u è lo spostamento assiale, v è lo spostamento trasversale e q è la rotazione dell’estremità considerata. Ogni matrice del tipo K*_ij rappresenta la matrice di rigidezza di un’asta connessa ai due nodi i e j , nella quale E è il modulo di elasticità del materiale, J è il momento d’inerzia baricentrico della sezione, l è la lunghezza dell’asta. Il significato di ogni termine della matrice di cui sopra prende un preciso significato:

K*_ij è la forza che nasce nel nodo di coordinate i, a seguito dell’applicazione di una forza unitaria nel nodo di coordinate j

In questo caso la matrice di rotazione risulta la seguente:

(16)

OSSERVAZIONE 6: la matrice di rigidezza presenta un dimensione tale per cui l’operazione tipo (10) riporta la matrice locale a sei gradi di libertà per elemento, allo stesso numero di gradi di libertà.

ASSEMBLAGGIO DI ELEMENTI FINITI BIDIMENSIONALI

L’operazione di assemblaggio per una discretizzazione mediante elementi bidimensionali (shell, plate) segue gli stessi principi di quelli mostrati nei punti precedenti.

Figura 5

Ad ogni nodo viene assegnata una numerazione locale, utile alla creazione delle matrici di rigidezza del singolo elemento; a livello globale ne viene assegnata una numerazione in base alla quale si possano eseguire la relazioni di equilibrio dei nodi appartenenti ad elementi differenti (Figura 5).