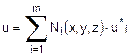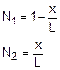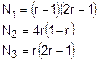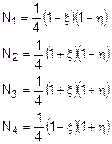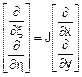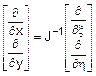· Meccanica Computazionale

· Metodo degli Elementi Finiti: Modellazione

· ELEMENTI FINITI E FUNZIONI DI FORMA

· Andrea Bacchetto

· INTRODUZIONE

· FUNZIONI DI FORMA DI ELEMENTI MONODIMENSIONALI

· FUNZIONI DI FORMA DI ELEMENTI BIDIMENSIONALI

INTRODUZIONE

La discretizzazione del dominio porta quindi alla generazione di nodi e di elementi finiti. I nodi, nelle applicazioni del metodo FEM, sono entità molto importanti in quanto la soluzione dell’intera struttura viene riferita ad essi: per estendere i valori del campo delle incognite su tutto il corpo vengono utilizzate delle funzioni che con la desiderata approssimazione riportano i valori nodali in ogni sottodominio.

Gli elementi finiti sono delle entità geometriche più o meno regolari caratterizzate da un determinato numero di nodi variabile a seconda del tipo di elemento. Tali nodi posso coincidere con i vertici degli elementi, ma in alcuni casi, ce ne possono essere alcuni disposti lungo i lati degli elementi stessi o addirittura all’interno. Un elemento quadrangolare, ad esempio, può avere un numero di nodi variabile da quattro (uno per ogni vertice) a nove (quattro ai vertici, quattro nei punti medi dei lati ed uno centrale). È evidente che all’aumentare del numero di nodi aumenta il grado del polinomio utilizzato per interpolazione dei dati ai nodi e, quindi, aumenta anche la qualità dell’approssimazione.

La scelta delle cosiddette funzioni di forma, che sono generalmente polinomiali (o comunque a comportamento noto) è un altro punto fondamentale che permette di ottenere una soluzione del modello FEM più o meno vicina alla realtà che si vuole simulare.

Al fine di rappresentare correttamente il valore ai nodi, le funzioni di forma devono assumere valori unitari nel nodo considerato e valori nulli sul resto dei nodi.

Il campo delle incognite per un problema di tipo tridimensionale può essere rappresentato mediante la seguente relazione generale:

(1)

Cioè a dire che il campo delle incognite è una funzione delle tre coordinate x, y, e z. Al fine di sfruttare il principio di approssimazione già introdotto precedentemente, si dovrà scegliere un insieme di punti in cui specificare esattamente le incognite (u*_i), mentre l’andamento della funzione è legato esclusivamente al comportamento delle funzioni di approssimazione N_i dell’elemento dette funzioni di forma:

(2)

Quindi solo le funzioni N_i dipendono dalla posizione.

FUNZIONI DI FORMA DI ELEMENTI MONODIMENSIONALI

L’esempio più semplice di funzione di forma è l’elemento finito lineare a due nodi dove le funzioni di forma sono di tipo lineare (vedi Figura 1):

(3)

Figura 1

Per un elemento lineare è possibile utilizzare anche funzioni di forma a grado più elevato, oppure le funzioni lagrangiane definite dalle seguenti formule:

(4)

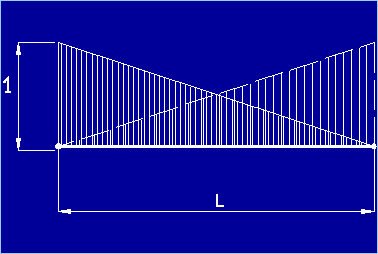
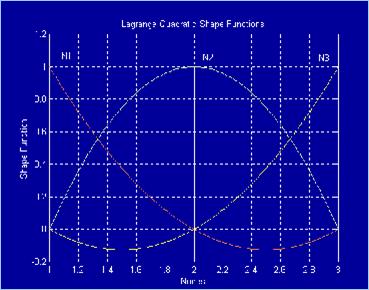
e rappresentate graficamente nella Figura 2.

Figura 2

È facile notare come le funzioni mostrate qui sopra assumono valore unitario nel nodo di appartenenza e nullo nel resto dei nodi.

FUNZIONI DI FORMA DI ELEMENTI BIDIMENSIONALI

Le applicazioni che utilizzano elementi bidimensionali sono molto ampie (assialsimmetriche, stati piani di tensione e deformazione, ecc.).

Secondo una formulazione isoparametrica degli elementi finiti, per l’esecuzione delle operazioni di integrazione al fine di valutare le varie matrici (di rigidezza, di massa, ecc.) utili all’assemblaggio, si ricorre ad una trasformazione di coordinate dalle generali (x₁,x₂) a quelli locali (x,h), per le quali il generico quadrilatero viene trasformato in un quadrato di lato 2 centrato nell’origine (Figura 3):

Figura 3

Per questa tipologia di elemento finito esistono vari gradi di approssimazione; per un elemento a quattro nodi si utilizzano delle funzioni bi-lineari che nello spazio di riferimento assumono le seguenti forme:

(5)

La trasformazione in coordinate locali risulta essere molto comoda in fase di integrazione sopra la superficie dell’elemento. I solutori ad elementi finiti hanno sviluppato una potente sistematicità e velocità che permette di calcolare gli integrali di tutti gli elementi dell’assemblaggio. Come tutte le trasformazioni di coordinate in fase di integrazione in più di una dimensione richiede il calcolo del determinate Jacobiano J della trasformazione. Tale calcolo risulta però particolarmente difficile da trattare dal punto di vista numerico quando la geometria dell’elemento originario presenta distorsioni notevoli come rapporti tra i lati molto grandi o angoli ai vertici tendenti o maggiori dell’angolo piatto (180°). In tali casi il determinante può risultare nullo o addirittura negativo, innescando una serie di problemi legati all’inversione della matrice della trasformazione. Le relazioni della trasformazione di coordinate sono espresse simbolicamente dalle seguenti:

(6)

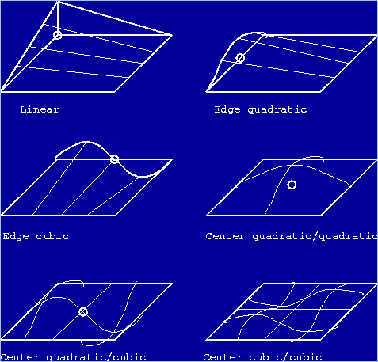
Si noti come la trasformazione (x,y) « (x,h) viene fatta sotto l’ipotesi di considerare un elemento isoparametrico. Altri tipi di funzioni di forma sono mostrati in Figura 4:

Figura 4